Generátory prvočísel
Eratostenovo sito

Eratostenes bol grécky matematik, geograf, astronóm, ale aj zememerač. Ako prvý odmeral obvod zeme, pričom jeho meranie malo odchýlku 5-15 percent v závislosti na tom, ako dlhá bola jednotka, ktorú používal.
Eratostenovo sito funguje takto:
- Napíšeš si čísla od 2 do n.
- Postupne škrtáš násobky najmenšieho čísla okrem čísla samotného (začneš násobkami 2).
- Po vyškrtaní všetkých násobkov 2 zoberieš ďalšie číslo so zoznamu, ktoré nie je škrtnuté, a vyškrtáš všetky jeho násobky okrem čísla samotného.
- Takto postupne vyškrtáš násobky všetkých neškrtnutých čísel až po číslo, ktoré je väčšie ako odmocnina n. V tomto momente zostanú neškrtnuté iba prvočísla menšie alebo rovné ako n.
Parabolické sito
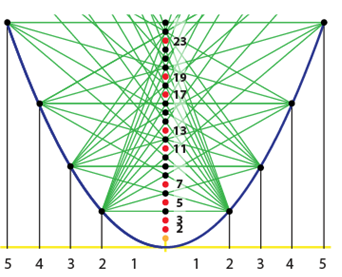
Pri tomto site sa najskôr urobí parabola tvaru y=x2. Potom sa urobia čísla na parabole, a to tak, že pre x 2,3,4... a -2, -3, -4... sa urobia body na parabole. Následne pospájaš úsečkou všetky body so všetkými bodmi na druhej strane. Čísla (do súčinu najvyššieho a absolútnu hodnotu najnižšieho čísla x, pre ktoré si urobil bod na parabole), cez ktoré neprešla žiadna úsečka, sú len prvočísla a číslo 1.
Sundaramovo sito
Toto sito funguje takto: Začneme s číslom 4. Potom urobíme prvý riadok aj prvý stĺpec tak, že každé číslo bude o 3 väčšie ako predchádzajúce číslo. Potom už iba dorobíme zvyšné riadky tak, že v druhom riadku bude každé číslo o 5 väčšie, v treťom o 7 väčšie, a tak ďalej, pričom to, o koľko sa zvyšujú čísla v riadku, sú po sebe idúce nepárne čísla. Keby boli všetky riadky aj stĺpce nekonečné, tak platí, že číslo 2n + 1 je prvočíslom vtedy a len vtedy, keď sa n nenachádza v žiadnom riadku ani stĺpci. Prakticky však musia mať riadky a stĺpce konečnú dĺžku. V tom prípade toto funguje pre všetky čísla do najvyššieho čísla na diagonále vychádzajúcej z ľavého dolného rohu alebo z pravého horného rohu (ak je horná strana kratšia ako ľavá, tak z pravého horného, ak je dlhšia, tak z ľavého dolného, ak rovnaká, je to jedno).