Rozhodovacie stromy

Algoritmus rozhodovacích stromov (angl. Decision trees) je jeden z najstarších a najpoužívanejších algoritmov. Najčastejšie sa využíva na klasifikáciu, ale jeho variant sa dá využiť aj na regresnú analýzu.

Stavba

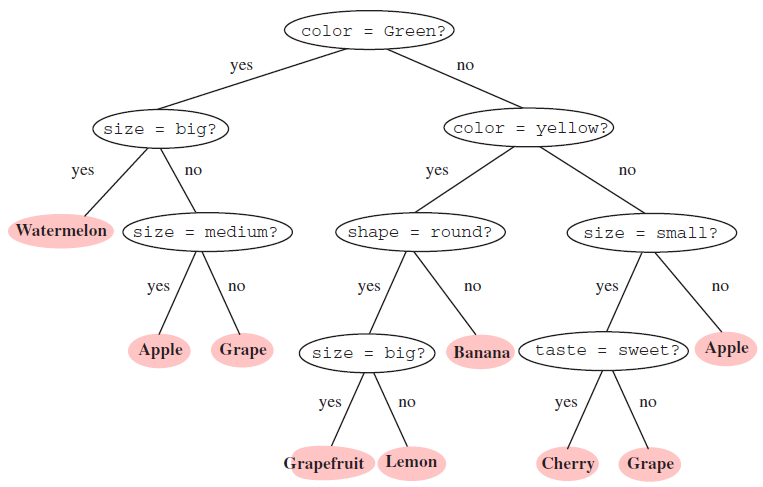
Rozhodovací strom (obr. 1) sa skladá z uzlov, pričom základný uzol sa nazýva koreňový uzol. Uzly sa ďalej rozvetvujú do ďalších uzlov a vytvárajú tak štruktúru stromu. Každý uzol predstavuje rozhodovanie podľa jednej vybranej vlastnosti klasifikovaného objektu. Vyberané vlastnosti musia objekty od seba čo najviac odlišovať, aby boli na konci stromu čo najpresnejšie klasifikované.

Výpočet

Pre správny výber atribútu, ktorý musí čo najlepšie rozdeliť dáta do dvoch čo najodlišnejších vetiev sa využíva informačná entropia a tzv. informačný zisk (angl. Information gain). Vzorec entropie je nasledovný:

$$-\sum\limits_i(P_i)\log_2(P_i)$$

• $P_i$ je zlomok príkladov v triede $i$ v tréningovej podmnožine datasetu

Ak je entropia pri použití $\log_2$ rovná nule, potom všetky príklady sú tej istej triedy. Ak je entropia pri použití rovnakého logaritmu rovná jednej, čo je jej maximálna hodnota pri tomto logaritme, príklady sú rovnomerne rozdeliteľné.

Príklad

Ako príklad môžeme použiť algoritmus na riadenie rýchlosti samoriadiaceho auto čisto len na základe slovných označení stupňa stúpania terénu, hrboľatosti terénu a prítomnosti rýchlostného obmedzenia. Výstupom tohto algoritmu bude slovné označenie rýchlosti auta, teda len rýchlo alebo pomaly. Skrátený dataset je znázornený v tabuľke dole:

Stupeň stúpania	Hrboľatosť	Rýchlostné obmedzenie	Rýchlosť
Prudký	Hrboľatý	Áno	Pomaly
Prudký	Hladký	Áno	Pomaly
Plochý	Hrboľatý	Nie	Rýchlo
Prudký	Hladký	Nie	Rýchlo

$P_\text{pomaly}$ bude zlomok hodnoty pomaly v rýchlosti, teda $\frac 24$, čiže 0.5 a to isté platí aj pre $P_\text{rýchlo}$. Po dosadení do rovnice a následnom výpočte bude entropia rovná 1. Rýchlosť teda môžeme použiť ako koreňový uzol stromu, pretože vyššiu hodnotu entropie ako 1 nedosiahneme. Ďalšie vetvy odvíjané od koreňového uzla sa však už budú riadiť informačným ziskom, ktorého vzorec je nasledovný:

$$\text{entropia}(\text{rodič})-[\text{vážený priemer}]\text{entropia}(\text{deti})$$

Entropia rodiča je v tomto prípade entropia koreňového uzla, a potom aj entropia každého uzla, ktorý sa bude rozvetvovať. Entropia detí je entropia ďalších vetiev odvíjajúcich sa od materského uzla, v tomto prípade od koreňového uzla.

Na výpočet informačného zisku pri rozdelení koreňového uzla cez stupeň stúpania potrebujeme najprv vypočítať entropiu detí. Po zakreslení vidíme, že vetva prudkého stupňa stúpania obsahuje dva výstupy s hodnotou pomaly a jeden s hodnotou rýchlo, čo znamená, že $P_\text{pomaly}$ tejto vetvy bude $\frac 23$ a $P_\text{rýchlo}$ bude $\frac 13$. Po dosadení do vzorca bude výpočet entropie vetvy prudkého stupňa stúpania nasledovný:

$$\frac{-2}3\log_2\left(\frac 23\right)-\frac 13\log_2\left(\frac 13\right)$$

Výsledok tejto entropie bude 0.9184. Výsledok entropie pri rovnom stupni stúpania bude 0, pretože sa v tejto vetve nachádza len jediný príklad, a tak sú všetky rovnaké.

Výpočet celkovej entropie detí bude:

$$\frac 34(0.9184)+\frac 14(0)$$

$\frac 34$ sú vo vzorci, pretože prudké stúpanie sa nachádza v príkladoch trikrát z celkového počtu štyri.

Informačný zisk pri rozdelení koreňového uzla cez stupeň stúpania bude:

$$1-\frac 34(0.9184)=0.3112$$

Pri pokračovaní vo výpočtoch ostatných rozdelení dôjdeme k tomu, že informačný zisk rozdelenia cez prítomnosť rýchlostného obmedzenia bude 1, čo je maximálna hodnota informačného zisku, a tak bude toto rozdelenie najvhodnejšie.