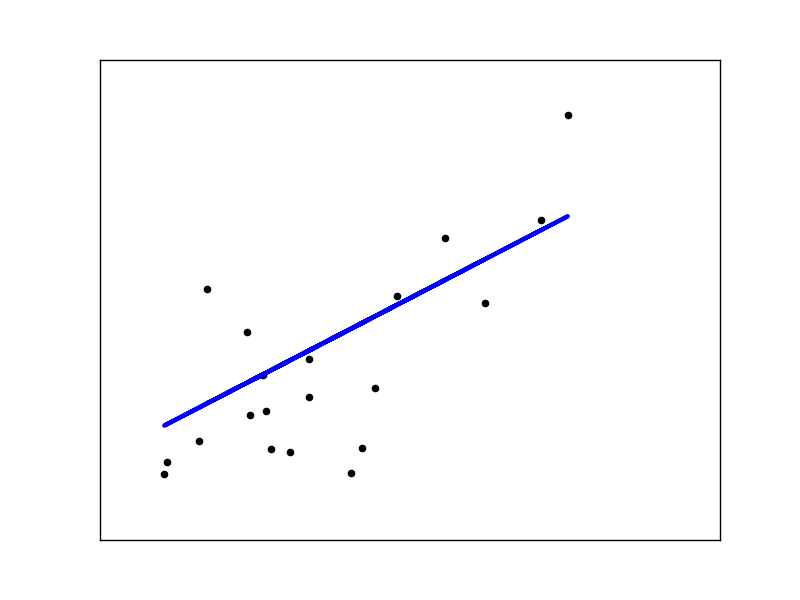
Lineárna regresia

Lineárna regresia (obr. 1) je najjednoduchší algoritmus regresnej analýzy. Na rozdiel od predchádzajúcich algoritmov, ktoré patrili ku klasifikačnému problému a vytvárali nespojitý výstup, lineárna regresia patrí k regresnému problému a jej výsledkom je spojitý výstup. Regresia vie určiť závislosť medzi vstupom a výstupom z tréningových dát a následne vie vypočítať závislú premennú, teda výstup.

Výpočet

Lineárna regresia vie vypočítať výstup pomocou nasledovnej rovnice:

$$y=ax+b$$

• $y$ je výstup lineárne regresie, teda závislá premenná.
• $x$ je vstup, teda nezávislá premenná, od ktorej závisí výstup.
• $a$ je prvok zvaný slope a vyjadruje sklon regresnej priamky na bodovom diagrame. Slope môžeme eventuálne nazvať aj ako rozostup medzi dátovými bodmi. Tento prvok zostáva pri lineárnej regresii rovnaký.
• $b$ je prvok zvaný intercept. Vyjadruje odskok začiatku regresnej priamky od nulového bodu. Ak je intercept rovný 0, tak sa regresná priamka bude začínať v nulovom bode. Ak je intercept napríklad 1, regresná priamka bude začínať v bode so súradnicami [1;1].

Príklad

Ako príklad môžeme uviesť vzťah medzi výškou a hmotnosťou človeka (graf 1). Použijeme vzorku 100 detí z datasetu výšky a hmotnosti 25 000 hongkonských detí. Tu regresia určila, že slope má hodnotu 0.6275 a intercept -50.001. Vstup môže byť napríklad 167.48 cm. Úlohou je určiť hmotnosť dieťaťa s takouto výškou.

$$y=0.6275\cdot 167.48-50.001$$

Výsledok je 55,09. Teda dieťa s výškou 167,48 cm, by priemerne malo vážiť 55,09 kg.

Minimalizácia chýb

Lineárna regresia hľadá najlepšiu regresnú priamku pomocou techniky minimalizácie súčtu chýb na druhú. V tomto kontexte je chyba technický termín, ktorý označuje rozdiel medzi skutočnou hodnotou dátového bodu a hodnotou predpovedanou regresnou priamkou. Súčet chýb na druhú sa označuje aj ako $r^2$ a dá sa zapísať pomocou nasledovnej rovnice:

$$\sum\limits_{i=1}^n(y_i-ax_i-b)^2$$

• $i$ je číslo dátového bodu, teda jeho označenie
• $y$ je skutočný výsledok
• $-ax-b$ je upravený vzorec funkcie lineárnej regresie

Cieľom funkcie lineárnej regresie je čo najviac minimalizovať $r^2$, teda čo najviac priblížiť jeho hodnotu k nule. Pomocou hodnoty $r^2$ sa taktiež určuje úspešnosť lineárnej regresiu, čo sa pri predchádzajúcich klasifikačných algoritmoch robilo pomocou techniky krížovej validácie.

Graf 1 (obrázkový formát pre pomalé pripojenia a menšie obrazovky)

Graf 1 (normálny formát pre rýchle pripojenia)